확산이란?
용매(solvent) A에 용질(solute) B가 고용되어 있다고 가정할 때 이러한 고용체 내에서 B성분 농도의 차이가 있다면, 시간의 경과와 함께, 농도차를 없애는 방향으로 성분B가 이동 하게 된다. 이러한 현상을 확산(diffusion)이라고 한다. 열역학적 관점에서 보면, 최종 안정상태에서는 고용체의 조성은 균일해져야 한다. 따라서, 확산은 B성분의 농도가 고용체 중에 균일해질 때까지 진행된다. Fick은 1855년 열전도의 이론을 이용하여, 확산을 지배하는 2개의 법칙을 찾았다.

Fick의 제1법칙
단위 면적을 가지는 가늘고 긴 봉형의 고용체 시료에서, 길이 방향으로 B성분의 농도 구배가 존재한다고 가정하자. 그림1과 같이 B성분의 농도를 c, 길이 방향의 거리를 x라고 하면, B성분의 농도구배는 dc/dx가 된다. Fick의 제1법칙에 따르면, 봉의 단위 면적의 단면을 통해 단위 시간 동안 확산하는 B성분의 유량(Flux, J)는, 농도구배 dc/dx에 비례한다. 이를 식으로 쓰면 다음과 같이 된다.

그림1과 같이, 농도구배가 dc/dx > 0 이 되면, B성분은 음의 방향으로 확산이 일어나기 때문에, 이를 고려해서 등식화 하면 다음과 같이 된다.
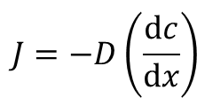
D는 확산계수(diffusion coefficient)라고 하고, 식의 상미분방정식은 1차원의 Fick의 제1법칙이다.
위의 식은 B성분의 확산유량J와 농도구배dc/dx의 비례관계를 보여주지만, 이러한 관계식을 이용하여 다음과 같은 간단한 실험으로 부터 확산계수 D의 값을 구하는 것이 가능하다. 그림2와 같은 두께가 d이고, 무한대의 면적을 가지는 순철의 박막을 고온으로 유지하고, 단면을 침탄성의 가스 분위기로 유지한 상태에서 반대쪽을 환원성의 가스 분위기를 만든다. 이때, 일정 시간 후에 정상 상태가 되고, 박판표면의 탄소농도를 침탄성 분위기 쪽에서 c1[mol/m3], 환원성 분위기쪽에서 c2[mol/m3]로 하자. 이 때, t[s]의 시간에 A[m2]의 면적의 박판의 표면에서 부터 환원성 분위기를 향해서 내뿜어지는 탄소의 양을 측정한 값이 q[mol]라고 가정하자. 여기의 관계를 위의 식과 같이 표현하면 다음과 같은 식을 얻을 수 있다.

따라서, 이 경우 확산계수는 다음과 같이 구할 수 있다.
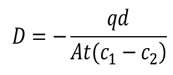
위의 식과 같이 확산계수를 구하기 위해서는 그림2의 실험에서 박판 양쪽의 분위기 내에서의 탄소의 이동속도가 박판 중의 확산 속도에 비해 충분히 빠르다는 가정이 필요하다. 이 가정의 성립 여부를 확인하기 위해서는 동일 온도, 분위기의 조건에서 박판의 두께만 다르게 했을 때 얻은 확산계수를 비교하면 된다.

Fick의 제2법칙
용질 성분의 농도구배가 존재하는 합금시료를 이용하여 일반적인 확산실험을 하게 되면, 그림2와 같이 정상상태가 성립하지 않고, 각각의 위치에 대해서 조성은 시간과 함께 변화한다.

그림3에 모식적으로 나타낸 바와 같이, 단면적이 A인 봉상 시료를 생각한다. x축을 따라 Δx의 두께를 가지는 체적요소의 한쪽에서 들어오는 유속을 J1, 다른 한 쪽에서 나가는 유속을 J2라고 했을 대, 만약 Δx가 충분히 작으면, J2는 다음식과 같은 전개식에 의해 J1과의 관계를 정의할 수 있다.
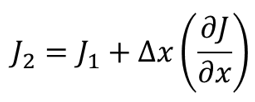
단위 시간 동안이 체적요소에 대한 용질의 유입량 J1과 유출량 J2는 다르기 때문에 체적 요소의 조성은 시간에 따라 변화한다. 체적 요소의 부피 V = A × Δx (단면적 × 두께)이므로 단위 시간과 단위 부피당 부피 요소의 순 물질 증가량 (∂c/∂t)는 다음의 식으로 주어진다 .

여기서 t는 확산시간이다. 두번째 식인 Fick의 제1법칙의 식은 농도 c가 위치 x의 함수로 주어진 경우, c의 시간 변화에 의존하지 않고 각 순간에 사용할 수 있기 때문에 이 식을 위 식에 대입하면 다음 식을 얻을 있다.

이 수식은 Fick의 제 2법칙이라고 부른다. 위 식은 합금시료에서 일어나는 확산 현상과 확산에 의한 상변태의 속도에 대한 수학적 분석에 유용한 표현이다. 다음은 비교적 간단한 실험 조건에 대한 Fick의 제 2법칙에 대한 답을 도출 방법으로 위 식의 수학적 취급을 단순화한다.

참고문헌
[1] Helmut Mehrer, Diffusion in solids
[2] Paul Shewmon, Diffusion in solid 2nd edition
'재료공학' 카테고리의 다른 글
| 금속재료의 강화기구 (Strengthening mechanisms) (0) | 2021.07.20 |
|---|---|
| 완전 결정(perfect crystal)에 전위(dislocation)이 도입되는 과정 (0) | 2021.07.20 |
| 알루미늄 합금의 석출강화 (Precipitation strengthening) (0) | 2021.07.12 |
| 전위와 슬립 변형 / dislocation and slip deformation (0) | 2021.07.12 |
| Binary Ag-Zn phase diagram (0) | 2021.07.12 |





댓글